[段考] 108下第1次段考-台北-北一女中-高一(題目)

108下第1次段考-台北-北一女中-高一(題目)

範圍：

　(※索取各種題目檔案請來信索取。)

---

一、單一選擇題(每題5分，共10分)

1. 已知三直線${L_{1}}$：${y=x}$，${L_{2}}$：${y=\sqrt{3} x}$，${L_{3}}$：${y=-x+3}$，其中${L_{1}}$，${L_{2}}$
   之夾角為${\alpha}$，${L_{2}}$，${L_{2}}$，${L_{3}}$之夾角為${\beta}$，${L_{1}}$，${L_{3}}$之夾角為${\gamma}$，，則：
   (1)${sin \alpha>\sin \beta>\sin \gamma \quad}$
   (2)${\sin \alpha>\sin \gamma>\sin \beta}$
   (3)${\sin \gamma>\sin \alpha>\sin \beta}$
   (4)${\sin \beta>\sin \gamma>\sin \alpha}$
   (5)${\sin \gamma>\sin \beta>\sin \alpha}$
   
   
2. 在${\Delta A B C}$中，若${\displaystyle{\frac{a+b+c}{\sin A+\sin B+\sin C}}=4}$，求${\Delta A B C}$的外接圓半徑
   (1)  ${1}$
   (2)  ${2}$
   (3)  ${4}$
   (4)  ${8}$
   (5)  ${16}$
   
   

二、多重選擇題(每題均有5個選項，至少有一個選項是正確的，每個選項2分，共20分)

1. 如圖，直角三角形${ABC}$，若${\overline{A C}=b}$，${\overline{B C}=a}$，且${R}$為${\Delta A B C}$之外接圓半徑，下列哪些關係式可用來表示直角三角形${ABC}$的斜邊長？
   (1)${\overline{A B}=\displaystyle{\frac{b}{\cos A}}}$
   (2)${\overline{A B}=a^{2}+b^{2}}$
   (3)${\overline{A B}=b \cos A+a \cos B}$
   (4)${\overline{A B}=2 R}$
   (5)${\overline{A B}=\displaystyle{\frac{\sin B}{b}}}$
   
   
2. 已知${\sin \theta=\displaystyle{\frac{12}{13}}}$，${\tan \theta<0}$，，下列有關廣義角三角比的選項何者正確？
   (1)${\tan \theta=-\displaystyle{\frac{5}{12}}}$
   (2)${\cos \theta=-\displaystyle{\frac{5}{13}} \quad}$
   (3)${\sin \left(90^{\circ}+\theta\right)=\displaystyle{\frac{5}{13}}}$
   (4)${\cos \left(180^{\circ}+\theta\right)=\displaystyle{\frac{5}{13}} \quad}$
   (5)${\sin \left(180^{\circ}-\theta\right)=-\displaystyle{\frac{12}{13}}}$
   
   

三、填充題(依下表答題格數配分)

答對格數	1	2	3	4	5	6	7	8	9	10	11	12
得分	7	13	19	25	30	35	40	45	49	53	57	60

1. 不使用計算器，求${\sin 150^{\circ} \cdot \cos \left(-45^{\circ}\right)+\tan 225^{\circ} \cdot \sin 330^{\circ}}$
   
   
2. 在${\Delta A B C}$中，已知${\sin A}$：${\sin B}$：${\sin C=2}$：${3}$：${4}$，且${\Delta A B C}$周長為${18}$，求${\cos C}$
   
   
   
   
   
3. 設${\sin \theta+\cos \theta=\displaystyle{\frac{1}{2}}}$，且${180^{\circ} \leq \theta \leq 360^{\circ}}$，求
   (1)  ${\sin \theta \cdot \cos \theta}$之值。
   (2)  ${\sin \theta-\cos \theta}$之值。
   
   
4. 設${\Delta A B C}$中，${\overline{A B}=5}$，${\overline{B C}=6}$，${\overline{A C}=4}$，在${\overline{A B}}$上取一點${D}$，使得${\overline{A D}}$：${\overline{B D}=3}$：${2}$，求${\overline{CD}}$之值。
   
   
5. 設${\theta}$為一標準位置角，且終邊在直線${3 x+4 y=0}$上，求${\sin \left(180^{\circ}-\theta\right) \cdot \cos (-\theta)+\displaystyle{\frac{3}{5}} \cdot \tan \left(180^{\circ}+\theta\right)}$之值。
   
   
6. 小綠某天通勤時發現北一女中的位置距離三個捷運站(台大醫院站、中正紀念堂站、小南門站)等距，且此三站不共線。小綠將北一女中設為極點，將三個捷運站的位置分別以極坐標表示。台大醫院站為$A\left[ r,{{70}^{{}^\circ }} \right]$，小南門站為${B\left[r, 225^{\circ}\right]}$，中正紀念堂站為${C\left[r, 320^{\circ}\right]}$，且台大醫院站到中正紀念堂站的距離為${750}$公尺。求北一女中到台大醫院站的距離(約至整數位)。
   
   
   
   
   
7. 如圖，梯形$ABCD$，${A B C D, \overline{A D}}$平行${\overline{B C}}$，${\overline{C D} \perp \overline{A D}}$，${\angle C A B=\alpha}$，$\angle CAD=\beta$，且${\overline{A D}=\overline{C D}=12}$，${\overline{B C}=7}$，求${\sin \alpha}$之值。
   
   
   
   
   
8. 如圖，已知正三角形${A B C}$紙片，邊長為${66}$，且${\overline{B D}=11}$。今沿著${\overline{A D}}$，${\overline{A E}}$兩線段將三角形紙片摺起，使得${\overline{A B}}$與${\overline{A C}}$兩邊重合，形成四邊形${ABCD}$，求：
   
   
   
   (1)  ${\angle D F E}$
   (2)  假設${\overline{C E}=x}$，求${\overline{D E}}$長度(不可以${x}$表示)
   (3)  求四邊形${ADFE }$面積
   
   
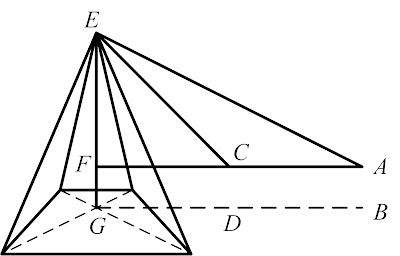
9. 小綠想要利用數學課所學的三角比，測量金字塔廣場的塔高，如圖：小綠一開始站在${B }$點，測量塔頂的仰角，得${\tan \angle E A F=\displaystyle{\frac{1}{2}}}$，接著小綠往前走了${4 }$公尺到${D }$點，再度測量塔頂仰角，得${\tan \angle E C F=1}$。已知小綠測量仰角時，眼睛離地$1.55$公尺，且$G$、$D$、$B$三點共線，求金字塔廣場塔高$\overline{EG}=$$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ }$。
   
   
   
   
   

四、混和題組

$2019$年${8}$月${30}$日${8}$時，第${18}$號號颱風中心位於台北東南方距離${450}$公里的海面上，以每小時${25}$公里的時速前進。

(1)  若颱風行進速度保持不變，但颱風行進方向轉為北偏東${15 }$度，試預測${24 }$小時後，即${8 }$月${31}$日${8}$時的颱風警報發佈時，颱風中心距離台北多少公里？(約至整數位)(5%)
(2)  若以台北市當作極點，正東方當作極軸，求${8}$月${31}$日時颱風中心之經緯度(約至一位小數)(5%)
(3)  若台北所在經緯度為東經$121.5$度，北緯$25$度，假設本題所敘述之範圍中，經距與緯距均為$100$公里，即在路徑圖上每一格代表$100$公里。試預測$8$月$31$日$8$時颱風中心之經緯度(約至一位小數)(5%)